
どうも、そいる塾長です。

今日も2018年3月7日に実施された京都公立高校中期選抜の問題をぱぱっと解いてみた感想を。
解きながら書いていきますので全体の感想・難易度は最後にまとめますね。
本日は第3科目の数学
全体概観
例年通りの形式。大問6に小問20。
ぱっと見た感じ例年通りの雰囲気です。
第1問:小問集合
難易度:易
はい、ここで16点。ここでとれないのは数学力でなく学習への姿勢な気がしますね。
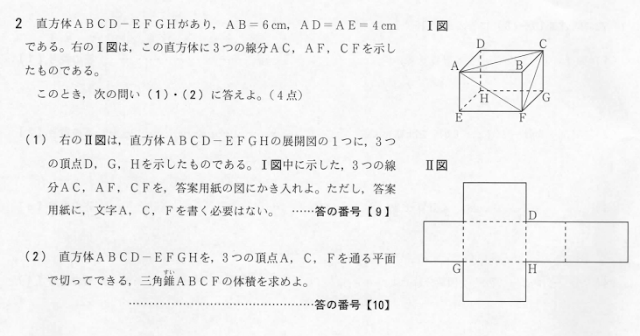
第2問:立体図形
(1)
難易度:標準
立体図形を問2で出してくるとは以外でした。
試験前に立体図形を回した紐の最短距離の問題を出題予想していたので展開図書くという点では当たったかな(笑)
立体図形が苦手な人には(1)の展開図は難しかったかなとも思います。
しかし丁寧に展開図に頂点を書きこんでいけば、必ずできる問題なんだけど、それでも苦手な人は頭で処理しようとしてパンクしてしまうんでしょうね。
事前の対策で「各問題を見たときに最初にどう動くか」ということをしっかり意識して勉強しておきましょう。
(2)
難易度:易
(2)が異常に簡単なので、最悪数学が苦手な人はそちらだけ取れれば良いかな。(2)だからどうせ難しいだろうと飛ばしてしまったならばそんな不幸なことはないですね(^_^;)
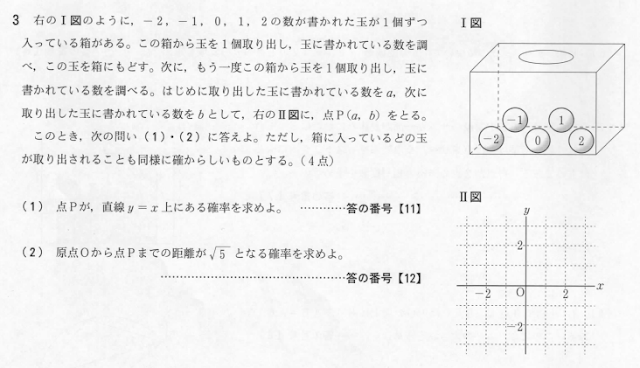
第3問:確率
グラフとの融合問題でひるんでいてはいけません。
ちゃんと入試対策を行った生徒でこのパターンがはじめての人はいないでしょうから簡単だったかと。
(1)
難易度:易
苦手な人でもグラフにy=xのグラフを書くなりしてx座標とy座標が同じであることを見抜けば良い。
(2)
難易度:標準
合計5個しか玉がないので、いくつか組み合わせれば距離が√5になる座標の組み合わせなどすぐに分かる。
数え方の方針さえたてばあとは丁寧に全パターン数えきるだけ。
これが出来ない人はとにかく手を動かすことを学んでほしい。実際に取り出した玉を書き出してグラフに書き込んで見る。
こういう「実験」を、手を使って行うと規則はすぐに見えてくるはずです。
確率・場合の数の問題は手を動かしながら考える!
来年は高校生ですからね。これが出来ないとやばいですよ。
第4問:1次関数
夏から鍛えた1次関数。いただきました。
もちろん何度か解いたパターンだったので私の生徒にはぜひ解き切ってほしいところ。
ただよくある係数がでかい式なので、いかに冷静に計算ができるかが勝負ですね。
こういうのも過去問演習時に想定しておいて欲しいところ。
(1)
難易度:易
できないとカンチョーです。
(2)
難易度:標準
数学が苦手な人は意外とこういうのが出来ない気がするな。
公式にはめるしか出来ないとつらい。4分遅れで出発し途中10分休憩し、残り何分よ?
で、同じスピードで行って帰ってくるんでしょ?小学生でも解けるんだけど、こういうのを問題パターンの暗記しかしてない子は解き方を脳内で検索しても出てこないんでしょうね。
(3)
難易度:標準
いつもどおりの最終問題。ちゃんと1次関数を勉強してきた人には、何の捻りもない典型パターンですので計算ミスがなければ満点狙えます。
もちろん解き方なんて暗記しておく必要はなく、「花子の現在地と、花子の一分後の弟の位置が同じ」というのを方程式で組めばよいわけで、初見でも解けなければいけないでしょう。
ここでも焦って計算がバグってしまうっていうのだけが心配かな。
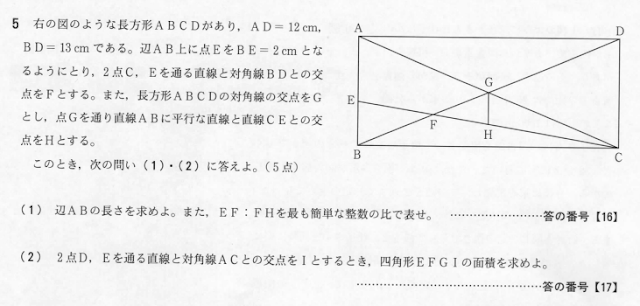
第5問:平面図形
ぱっとみて相似だな、面積比だな!とわかるので攻め方で戸惑うことはないでしょう。
それ以外何をしろと?
(1)
難易度:易
相似を全く見たことも聞いたこともない人でなければ、どう見ても相似の典型パターンが見えると思います。
(2)
難易度:標準
いつも指導している通り四角形の面積をどう処理するかで血迷わなければ答えまでたどり着ける。
いくつか方法はありそうだが、線分EGに補助線引いて四角形を2つの三角形にわけるのが一番素直で計算がスッキリかな。
あとは底辺の比で面積を出していけば良い。途中「比の合成」があるけど、いまさら出来ないほうが悪い。
やはりこのへんが出来ない人は必要な知識だと分かっていて放置しているのですから解けなくても仕方ない。
そういう人は(易)の問題だけといていれば20点。それで十分志望校には通る。
ちょっと冷たいですが、数学のセンスなどではなく、ちゃんと勉強したかが問われる問題。こういうところで差がつく。
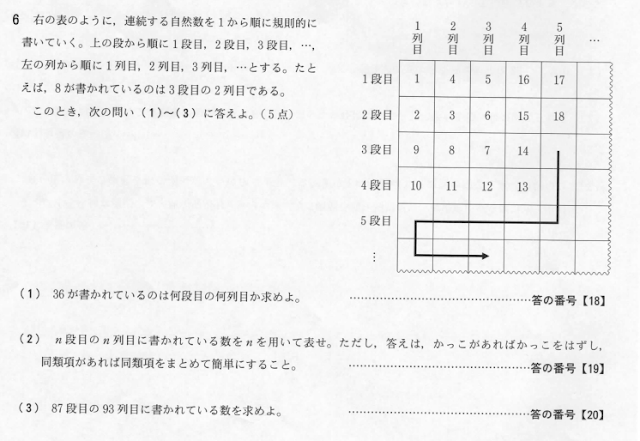
第6問:規則性
最後はお決まりの規則性。
たしか昨年は等差数列と等比数列でしたっけ?とりあえず瞬殺だったので、今回は少し考えないといけないので難易度アップでしょうか。
(1)
難易度:易
とりあえず数学が苦手な人は残り時間でお絵かきして(1)で1点頂いて終了。
(2)
難易度:難
問題は(2)から。
いくつか解き方はあると思います。
ここから式に持っていけるかどうかが数学力。
下の①②、こっちは中3生に指導するならちょいと邪道かなと。
本来は③で解く問題なのかなと。高校入試の王道規則性と言った感じでしょうか。
表から規則を読み取れるかの勝負。ただ王道は王道なので解けた人も一定数は確実にいるはずです。
解法①

階差数列っすよね、おれ進学塾で習ってるんで知ってるっすよ。
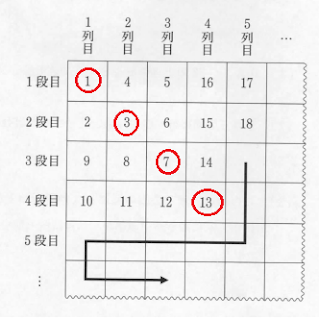
(2)はn段目n列目を出せと言っているので素直に、対角線上に1,3,7,13,・・・という数列に規則性があることをもとに解く方法。
これを高校では階差数列として習います。つまり高校生なら公式に当てはめて瞬殺できます。
高校生の先取りをしておけば簡単ということですね。(笑)
これは知ってるだけの話なので数学力ではないな(笑)。却下。
前期選抜でも「重心」知ってたら瞬殺みたいな問題がありましたね。
そのへん問題作成者には意識してほしいな。こんなんおもしろくないやん?
あくまで知らないけど解けるを見たいんだし。反則とはいわないけどこれで解けることを自慢するのはちょっと違うな。
まあ、「試験中に階差数列の公式を導き出してしまいました」みたいなやついたら大好きすぎるけど。
解法②

数字の並び方みれば式くらい思い浮かぶっす。
これも上の階差数列を使うわけですが、階差数列として処理しないという解き方。
地道に列番号(段でも一緒ね)からこの階差数列の並びになるよう「こねくり回して」いけば見えてくる。
つまり表から斜めに、1,3,7,13,・・・と抜き出して1段目は1,2段目は3、3段目は7・・・と考えて「こねくり回す」
「2を二乗して1引けば3」「3を二乗して2引けば7」「4を二乗して3引けば13」⇒「nを二乗して(n-1)を引けば…」みたいな。
数字で実験して文字式に一般化する方法ですが、これは最後の手段ですな。
ちなみにわたしは結構すぐ思いついたので暇な人はやってみてね。まあ階差数列だってわかってるから思いつくのかもしれないけどね。
解法③

いやいやせっかく表が載ってるんで活用しようず。
次の(3)を見たら気がつくと思うんですが、多分これが模範解。
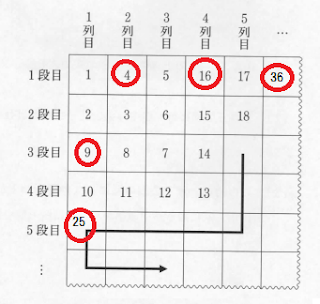
横方向(列)は偶数番号、縦方向(段)は奇数番号に注目すればもうおわかりですね。
2列目(1段目)が4 ⇒ 3段目(1列目)が9 ⇒ 4列目(1段目)が16・・・てな具合に表の偶数の時はn列目(1段目)のを、奇数の時はn段目(1列目)のを見ていけば「nの2乗」という簡単な規則性が見えますね。
(あ、1に丸するの忘れてる…)
そこからn段目、n列目を考えていくと、nが奇数ならn段目(1列目)から右へ1ずつ減らすのでn列目は【-(n-1)】すれば良いし、偶数ならn列目(1段目)から下へ1ずつ減らすのでn段目は【-(n-1)】すれば良い。
これが一番スタイリッシュですよね。
(3)
難易度:標準
(2)さえ突破できれば(3)は簡単。しっかり規則を見抜いて「93列目は奇数番目だから下に降りてくる」という規則を見落とさず(2)で出した式に代入して計算ミスさえしなければ、あとは指折って数えるだけで済む話。
ま、この問題見たら上の③で解くべきなのは明白ですね。
まとめ 難易度は昨年並
間違いなく今回の数学で最も正答率が低い、つまり難易度が高いのは第6問だったと言えますが、全体としては昨年と同様の基礎レベル。
もしくはやや易化か。2年前の難化は一体何だったんだという感じですね。
円周角も二次関数も出ない。立体図形もそれじゃない感…。完全に肩透かしでした。
この辺が出ないのは今年だけだと思うので、出ないなら出来なくてもいいや!なんて錯乱しないでほしいのですが、難易度はもうこの感じで落ち着いてくれるのかな…?
このレベルだとこれまでよりは他科目と得点分布が近くなるんじゃないでしょうか。その分、できる子とできない子の得点差が出そう。
しかしちゃんと基礎レベルさえ固めていれば8割近くまでいけそうなので、次年度受験生の皆さんで中期本命の方は、基本をしっかりと学んでいきましょう。
それにしても、もう少し中学生たちには計算スペースを与えてもいいのでは?
他科目同様問題冊子の紙をケチりすぎている気がします。
今日はこのへんで。





コメント