
どうも、そいる塾長です。
今年は昨年と比べどうだったでしょうか?順番に解きながら書いていきますね。
昨年度の記事はこちら。
2019年度前期選抜の数学

問題は京都新聞社さんのサイトからダウンロード可能です。
全体概観
50分で50点満点。
問題の順番が2と3で昨年と確率と関数の位置が変わったくらいで、見た目の変更は特になし。
記述式の証明問題の配点が3点→4点になったところぐらいでしょうかね。
あ、今年はヒストグラムが出なかったのか。ぐらいですかね。
問1:計算・小問集合
難易度 (1)~(9)易 各2点
問2:確率
難易度 (1)易 2点 (2) 易 2点
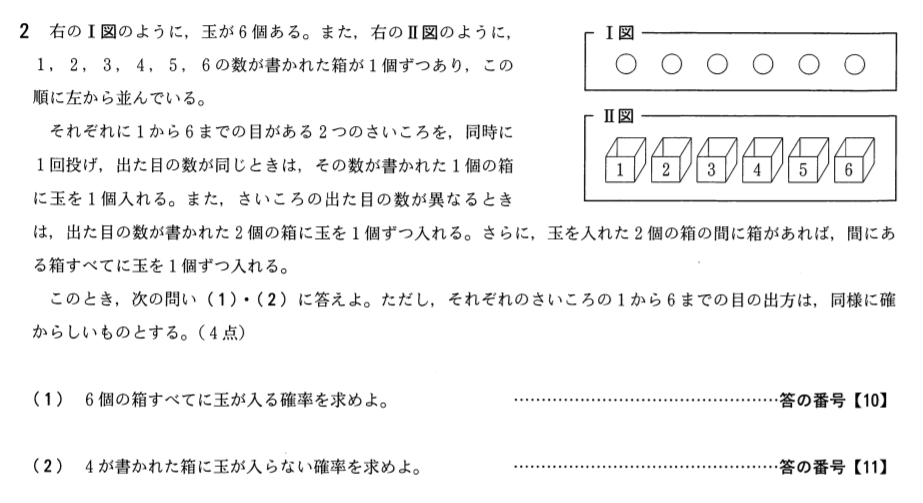
(1)は超基本問題。確実に2点を。
ただ、今回の問題も確率ではよくあるそ「それやって何が楽しいの?」という意味不明なゲームにつきあわされるので、問題文をしっかり読んで”見慣れない”ルールをちゃんと把握できるかだけのお話です。
ちゃんと頭の中でサイコロ降って問題文に乗っている絵をみながら”実験”してみようとするかどうかです。
問3:関数
難易度 (1)易 2点 (2) 易 2点 (3)標準 3点
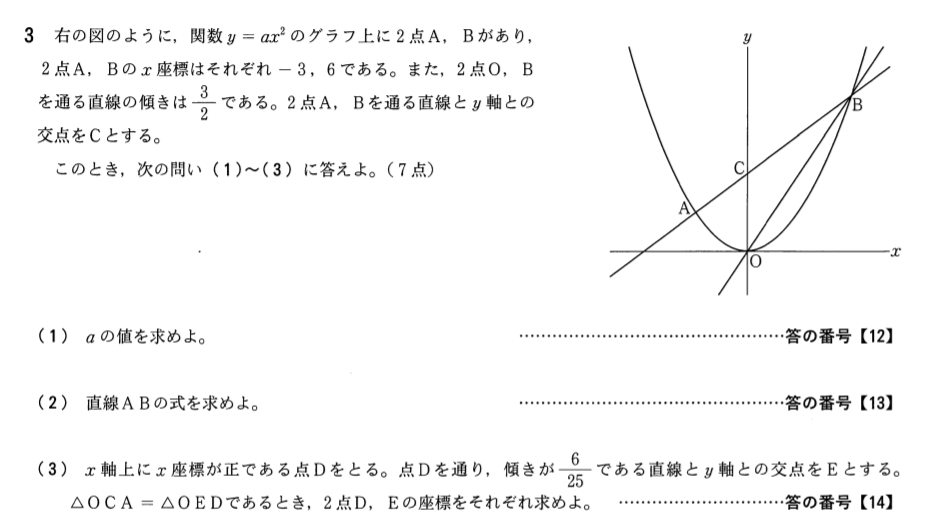
(1)(2)は超基本問題。確実に4点を。
(3)に関してもグラフ上で面積を求める何回見たか分からないくらいの定番のかたち。
昨年の関数の問題よりもオーソドックスかなと。
問題にD,Eの点が図示されていないので自分で問題文を読み取って図示できるかどうかだけですね。数学が苦手な子にはこのハードルが結構高いのですが、別に読めないんじゃなくて読まないでの子が一定数いるのがね^^;
3点ということもあり、完全解答ながら片方解ければ自動でもう片方も出せるので、今年の関数の(3)は絶対に落としたくない問題。
問4:立体図形
難易度 (1)易 3点 (2)難 3点[1・2点] (3)やや難 2点
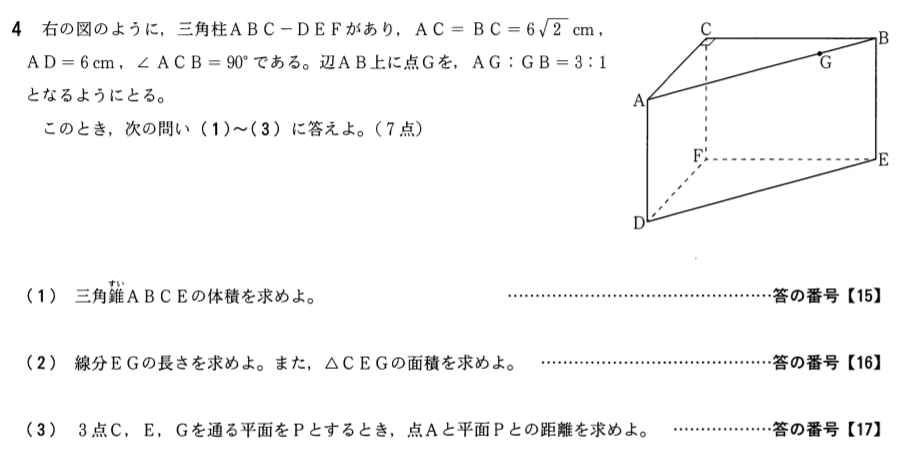
(1)で三角柱の体積求めている不幸な子がこれまた一定数おりそうな…さすがにいないか^^;
(1)と(2)のEGの長さだしたら数学苦手な子は次の問題へすっと移れたかどうかが大事ですね。これだけで4点もらえます。
△CEGの面積は難しい。
まずは三角形ACBを抜き出してあげてこんな図を書く。(Cから辺ABにおろした垂線とABの交点をHとでもしておきましょうか)
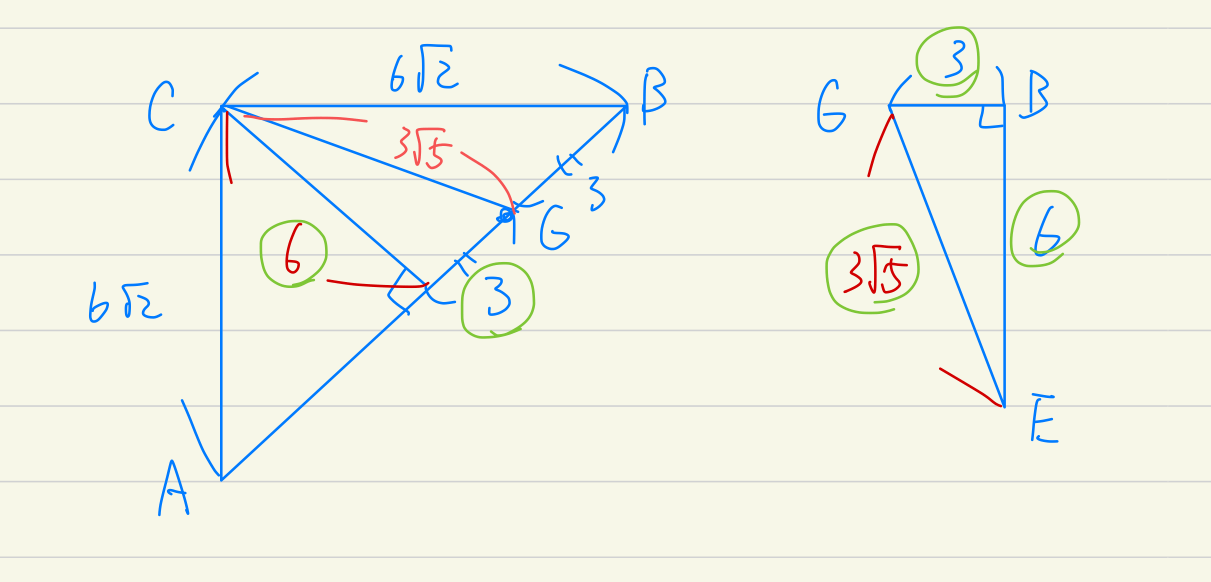
そうすると△CHGが△EBGと合同だとわかります。
よってCG=EGとなるので△CEGが二等辺三角形だとわかります。
ここまでわかれば勝負ありです。あとは三平方の定理でCEの長さを出して、またまた三平方の定理で変CEを底辺にしたときの高さを出してハイ終了!です。
う~ん、なかなか難しい。三角形ABCを書き出さなかったら気が付かなかったかな。勘で△CEGが二等辺三角形だと見抜いて解けちゃった人もいるかもしれませんが。
(3)に関しては(1)で出した三角錐をもとに3:1の比を使って△ACGの面積を出しておいて、三角錐A-CEGの体積だしてAから平面Pへの距離を高さにして(hとでもおいて)方程式という、空間図形お約束の問題パターンですので簡単。これは確実に昨年よりは緩い。
勝負は(2)の△CEGの面積ですね。
問5:平面図形
難易度 (1)標準 4点 (2)難 3点 (3)やや難 2点
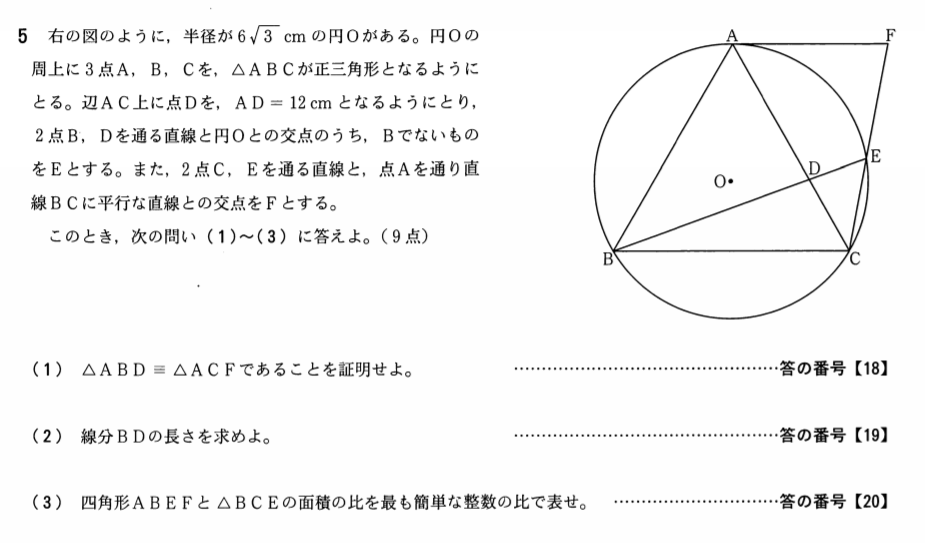
(1)で今年も記述式の証明が出ましたね。
出るの分かっているんだから大丈夫でしょう。合同なんでお約束のパターンで書くだけです。こういうのを記述式って言ったところで感がありますがね…^^;
京都の公立入試の特徴なのか情報を自分で図にしっかり書き込んでいく必要がありますが、問題文から「正三角形」「平行」の2条件を読み落とさず、「これどう見ても円周角でしょう」ということにさえ気が付けば瞬殺で合同条件が見つかりますね。配点が4点と大きいですし、なにがなんでもしっかりとっておきたいところ。
中学生が「証明が苦手です」と言う場合、多くは証明が苦手なんじゃないんですよね。また詳しくは別のところで書きますが別に原因があるんでね…。
なので苦手とかしていないでしっかりやっておきましょう。高校行ったら死ぬ…よ。
(2)がなかなか難しい。他にも解き方がありそうな匂いがプンプンしますがとりあえず最初に思い付いた解き方を。わかりにくいので解くときに書いた図を載せておきます。
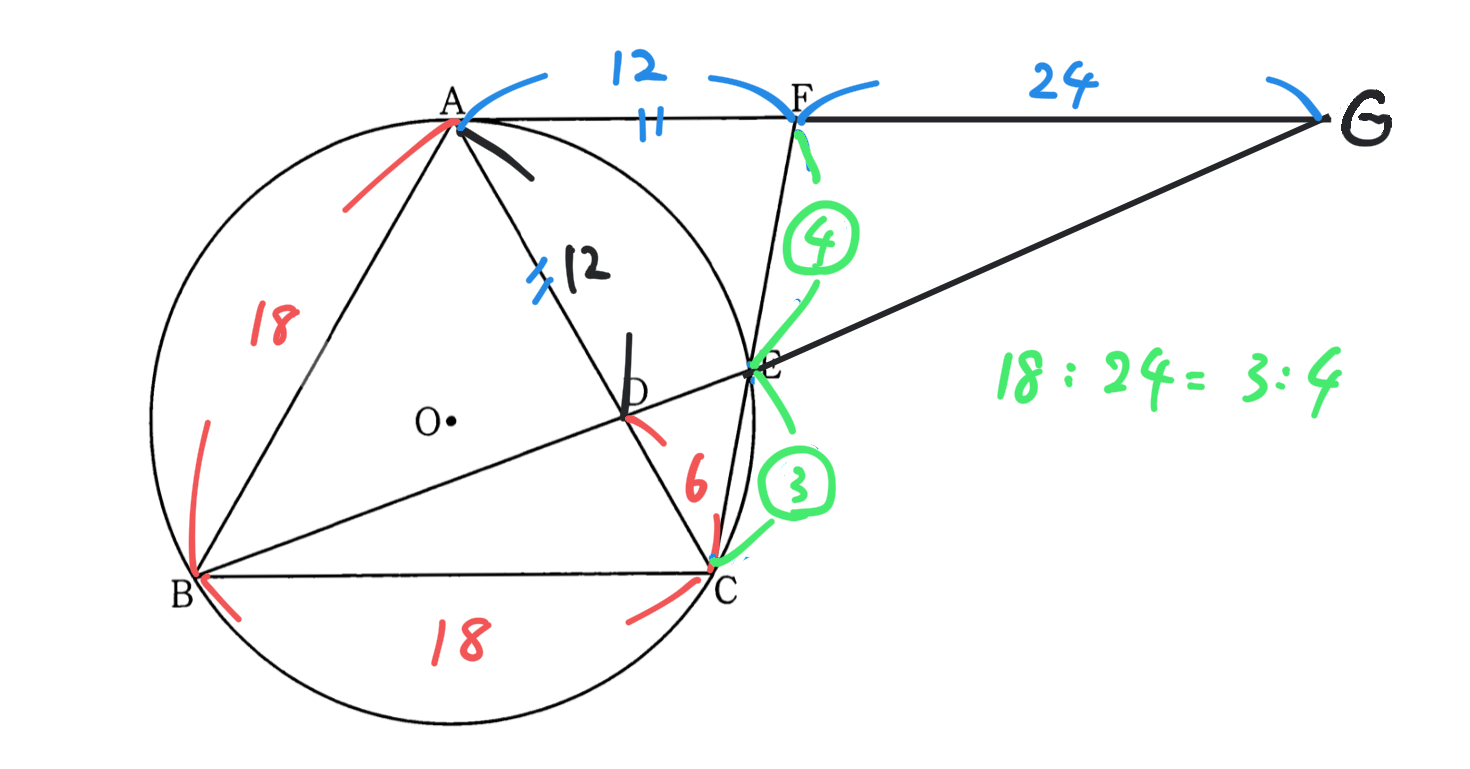
※上の図はあくまでメモなのでその辺ご了承ください
(1)の合同を使えという啓示を聞きのがさないようにして半径から三平方で正三角形の1辺の長さを出し、AD=12→DC=6なので下の図のようにAFの延長線とBEの延長線の交点をGとおいて三角形BCD∽GAD(相似比1:2)FG=24をだしてからの△BCE∽GFEに目を移してBC:FG=18:24
てことでCE:EF=3:4が導けます。ここでCFの長さをXとでもおいて△CDE∽CFAの相似を利用して6:X=3/7X:18。これを2次方程式にして解いてあげるとCF(=BD)の長さが出てきますね。
う~ん、もっと簡単な方法がありそうな気がしてならない^^;
この解答が模範解答だとするとだいぶ入試問題慣れしていないとAFを横に伸ばそうと思わないですよね。なんせ今回のは問題用紙の外にはみ出ちゃうので^^;
このパターンは入試問題としてはよく見るやつですがそれでも難しいかなと。
(3)に関しては(2)さえクリアできていれば難しくはないですね。
どこかを基準(私は△ABDにしました)にして底辺の比と相似比を用いて拡張、等積変形していけば面積比でおしまいのお決まりのパターン。四角形ABEFに関してはここでも(1)(2)で出した答えを使うのさえ忘れなければ難しくはない。
ということでこれも勝負は(2)です。
問6:規則性
難易度 (1)易 1点 (2)標準 2点 (3)やや難 2点
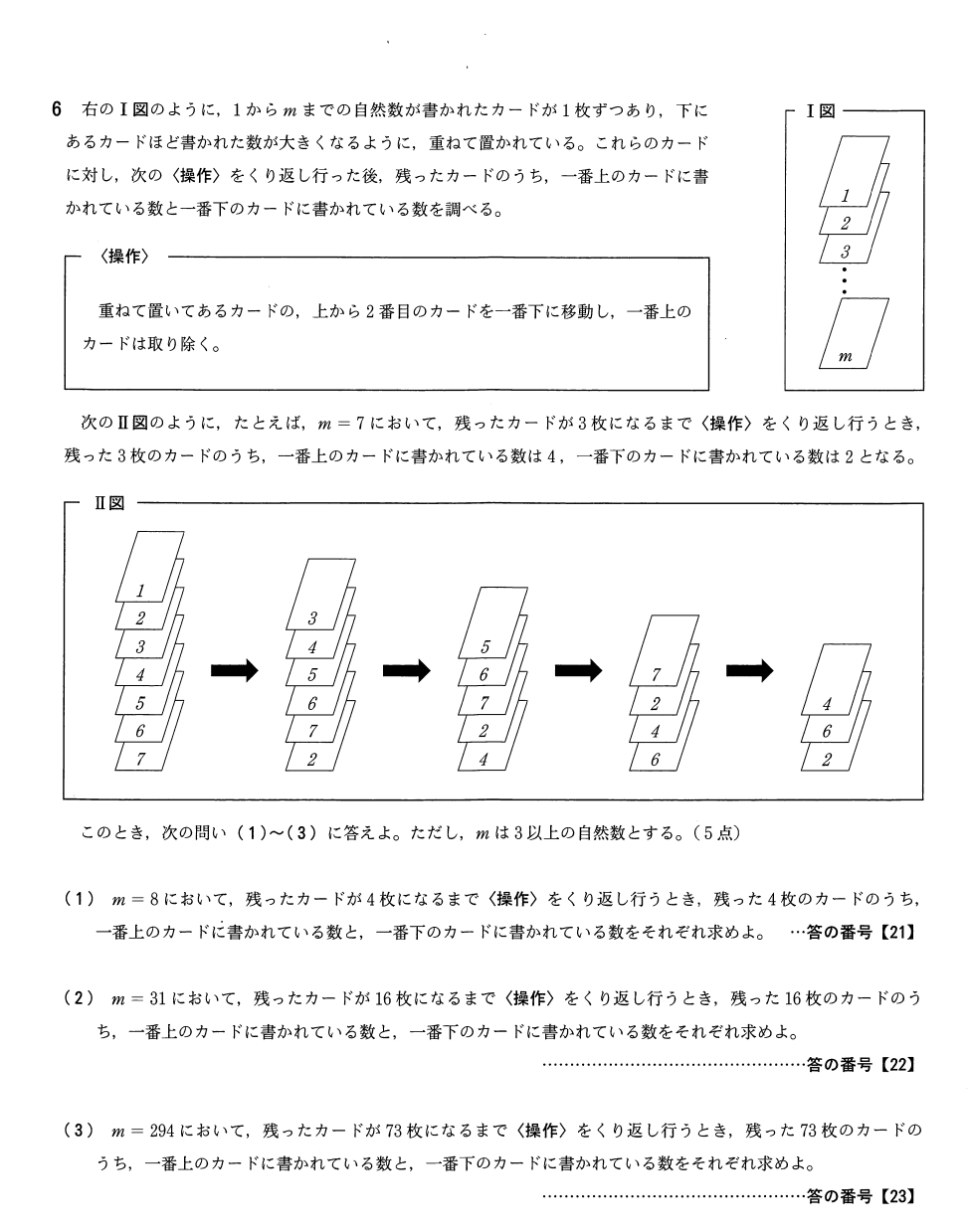
最後はお約束の規則性の問題。
(1)書けばわかるので死守。
(2)からは規則性を見つけてあげないと厳しいですね。
親切に問題に図が載っているわけですから、一番上のカードが「1,3,5,7・・・」となっていることに気が付くでしょう。
となると…
m=31なら残りが16枚になるのは15回操作した後。つまり1に15回2を足せばいい。
となると…
1+2×15=31
この計算式を一般化しておくと後で楽ですね。
n回操作を繰り返すとすると…
これは後々使います。
…となるので(2)の解答はこの計算で出ますね。一番上のカードは31。
で、そのときの一番下の札は最後の15回目の操作で一番下にまわされた札なので偶数の札ですね。
ひとつ前の操作では一番上から「29、30、31…」になっているので一番下に回った札は30と。ここまでは楽勝でしょう。
(3)に関してはm=294ですが、(2)での規則をもとに考えると…
m=294なら残りが73枚になるのは221回操作した後。つまり1に221回2を足せばいい。
となると…
1+2×221=443
となるので一番上のカードは443。
443… (゚Д゚;)
とはさすがにならないでしょうか(笑)
(1)でこの2周目突入パターンは問題が教えてくれていますからね。
ちゃんと誘導に乗ることができるようになりましょう。
では、この最初に一番下にあった294が一番上(実際は上から2番目)まで来て(1周目)、再度一番下に戻っていく(そのあとが2周目)パターンを考えてみましょう。
全部の札の中で一番大きな奇数が293なので、1周目の最後が「293,294,2,4,6,8…」となる状態。奇数の293が一番上に来ているので先ほど式に代入して考えてみると
2n+1=293
ということでn=146
これが146回目の操作後の状態だとわかりますね。
で147回目の操作後「2,4,6,8,・・・,294」となりここから全部の札が偶数になり、規則が変化します。
ここからの操作で一番上に来る数字を並べてみると…
2→6→10→14→・・・
4ずつ増加していくだけの規則ですね。
なので先ほど作った計算式をここで変更します。スタートが2で4ずつ足していくので…
あと残っている操作の回数は221回ー147回=74回
となれば2に74回4を足せばいいだけの話です。
てことで2+74×4=298
298が一番上に来ていることが分かりましたね。
(゚Д゚;)
終了…と思いきや298…。また超えちゃいましたね^^;
てことでその1個前の220回目の操作後に戻してみましょう。
298から4を引くだけですね。
「294、4、8、12・・・」となっているはず。
でここから”手動”で操作してみましょう。
そうすると、294の札が捨てられ、4が一番下に回り、8が一番上に来るわけです。
てことで、模範解答となるわけですね。
とまあ、中学生が解くならこんな感じでしょうかね。等差数列の公式みたいなのを使っていますがあくまで公式は知りませんという前提で。あんなのを塾で教えてもらって秘密のテクニックを教えてももらったと思っている時点で数学オワタになりかねんので注意を。
規則性の問題の難易度としては昨年と同じくらいでしょうか。
場合分けがめんどくさいですが図形要素がなく数字遊びだけで解けるので今年の方がやや簡単かなとも思いますが。
まとめ
昨年と同じく図形の難易度が高め。図形を制するものが前期の共通問題の数学を制する感じでしょうか。制したところでどうなるってもんでもないですが^^;
逆に言うと数学が苦手な人はそれ以外でしっかり対応できる基礎力を身に着けておかないといけませんね。
最初の小問集合と各問題の(1)は本当に基礎中の基礎なので取りこぼさないように。
さらに中期選抜が現在易化傾向ですので、普通科志望の方は難しい図形を勉強するより基礎を落とさないことをまずは第一に。今回私が標準とした問題ですね。少し数学が得意ならやや難まで対応できれば十分差をつけられるのではないでしょうか。
ただしここで言う難や標準と言うのは共通問題ではと言う意味です。解けないとかって意味ではありませんので。
なお「易」とした問題をすべて正解すると30/50点となります。6割ですね。ここが最低レベルと思って勉強しましょう。これ以下は勉強していません。理解していようが丸暗記だろうが何だろうが取れる問題です。
平均点は昨年と変わらないような気がします。(お願いだから公表して^^;)ただ図形は(2)がストッパーになっているのでその分ちょっと昨年より低くなるかなと。
という感じで以上「2019年度前期の数学解いてみた」でした。
やっぱり動画とったほうが早い(笑)
せっかくなんで声がかれているのが治ったらやってみます。
今日はこのへんで。





コメント