
どうも、そいる塾長です。
国語に引き続き、2018年2月16日に実施された平成30年度京都公立高校前期選抜の問題をぱぱっと解いてみた感想を。
※以下、詳しく解説はしていませんが、問題画像とともに着眼点などには触れていますのでネタバレが困る方はご遠慮ください。
本日解いたのは「数学」

全体概観
難易度は昨年並かやや易化と言った感じかな。
30点まではいつも通り簡単に到達できます。そこからが勝負ですね。
問2以降のいわゆる(3)=最終問題の難易度もそこまで高くなかった感じですが、解法パターン丸暗記で数学を乗り切って来た人が詰んでしまうような、発想の転換が必要かなと思われる問題が多く見られました。
基本的に京都公立入試の数学は前期でも中期でも他科目に比べ難易度が高い。
ただし約6割は超絶基本問題から構成されています。
つまり数学での最初の勝負は基本問題の30/50点。ここがデッドライン。
正直言って学校ワークや塾テキストの確認問題・基本問題のみしっかりやっていればこの30点はとれる。
しかしそこからは急激に難易度が上がるので、30点⇒40点、40点⇒50点はなかなかに厳しくなります。
生半可に問題集の入試問題をこなすだけでは時間を使うだけで点数には跳ね返ってきません。
それなら他科目に時間を回したほうが合格可能性は上がるかもしれません。
それどころか応用問題にばかり目が行き、解けもしない問題に時間を使い基本問題でミスをしてしまえば30点を下回り取り返しのつかないことに。
では各問題を見てみましょう。
難易度は標準的な生徒を基準に私の主観で判断しています。(結構適当です笑)
あと30分位で解きましたんで他にもスタイリッシュな解法があるかもしれませんが最初に思いついたものしか書きません。書けません、お許しを。
問1:計算・小問集合
難易度 (1)~(9)易
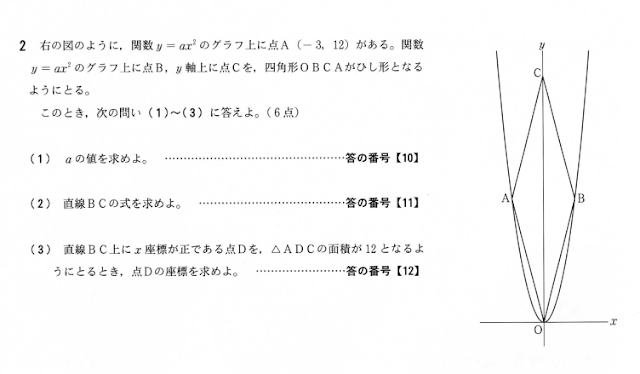
問2:関数
難易度 (1)易 (2) 易 (3)やや難
(1)(2)は超基本問題。確実に4点を。
問題は(3)。面積を求める三角形は関数の問題では何回見たか分からないくらいの定番のかたち。
ところがいつも通り求める座標を文字でおいて…とやってしまってパニック!となってしまった人も多かったのではないでしょうか。
発想の転換が必要です。
図形問題と捉えれば、相似と面積比で瞬殺できます。
こういうの好きです。
解法パターンの丸暗記は定期テストでは強いかもしれませんがこういう問題では見えるものを見えなくしてしまうんですよね。
ですが、生徒は目の前のテストを如何に楽して点数を取るかしかみていない。
こういうのを早い段階で思い知らせておきたいですね。
この(3)は見えてしまったら暗算で10秒位で解けます。そういう意味では簡単な問題ですね。
問3:確率
難易度 (1)易 (2)やや難
(1)は日本語が読めて丁寧に書き出せばそれで済む問題。出来なければいけませんね。
一方で(2)は数学が苦手な人にとっては8の倍数⇒因数が(2・2・2)という発想ができないかもしれません。
ここだけなんで正直解けないといけませんね。
あとは丁寧に数え漏れがないように一枚のカードを固定しながらしっかり数えましょう。
問4:平面図形
難易度 (1)標準 (2)易 (3)やや難
(1)(2)は基本問題。
(1)は記述式だから標準としましたが、だからといって怯んでしまってはいけません。
定期テストでも絶対にできないといけないような基本レベルしか今のところ前期選抜の記述問題では出題されていません。ここでも確実に2点を。
問題は(3)ですがここでは(1)や(2)で出される証明問題は(3)のための誘導ということを思い出してもらえれば簡単ですね。
ぜひ完答してもらいたいところ。
(ちょっと問題文が気になるところがあるが気のせいかな?)
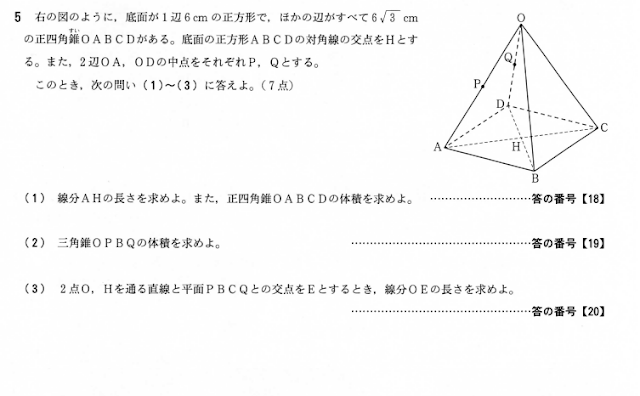
問5:立体図形
難易度 (1)易 (2) やや難 (3)やや難
(1)三平方の定理で超基本問題。
(2)はよくある切断問題ですが、イメージしやすく簡単だったかもしれませんね。
立体図形は見たら飛ばすと言うくらいアレルギーのある方も多いですが落ち着いて解いてほしかったところ。
体積ですので「高さ」を求めようと必死で探して詰んでしまった人は発想の転換を。
私が指導している通り、基本に忠実に△OAD平面を抜き出して図化すれば相似比から(底)面積比へつなげて瞬殺できる問題だと気づけたはず。
(3)も同じくPBCQ平面を抜き出し「重心」の問題だと気づけば解き慣れた子なら計算もせずに瞬殺できたはず。
重心をおぼえていなくても、これまで数学の入試演習をしっかりやって来た人なら問題集で絶対に出会っているはずの定番問題なので出来てほしいところです。
そう言えばついこないだも質問されたばかりでした。ちなみにその子は受けてませんが。
努力の成果が試されたと言いたいところですが、(2)で詰まった人は無念でしょうね。
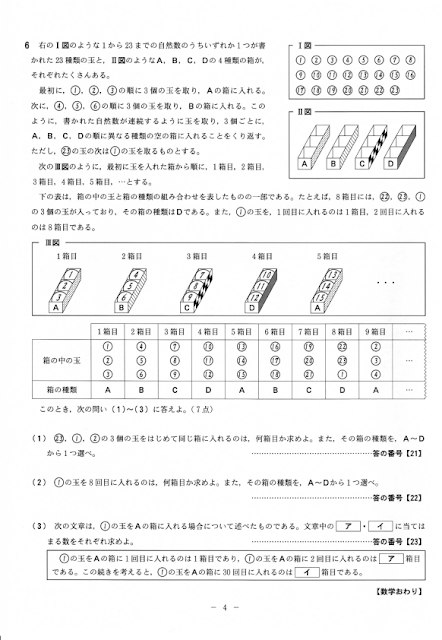
問6:規則性
難易度 (1)易 (2) やや難 (3)難
(1)(2)ではまずは箱の種類は気にしなくて良いので、「8箱周期」で数字が移動する問題ということに気がつけば簡単。あとで4箱周期でどの箱か考えれば良いです。
ただ毎度のことながら長ったらしい問題文見て捨てちゃった人も多かったかなと言う気がします。
去年は電球とスイッチ、おまけに指数の見た目で戦意喪失した子もいましたね。
某中学で数学トップ(とは言っても数学は得意ではない子)は解説した後「な~んや」って言ってました。
とはいっても本番にこのレベルが落ち着いてしっかりと解き切れる子はなかなかいないと思います。
そういう子は多分専門学科を受けていると思うので(笑)
こういう複雑な問題設定をしっかり読み取る力って大事ですよ。現代文や社会の資料の読み取りとかと一緒です。
読解力というより情報分析力ね。これは国語で鍛えるより数学で鍛えた方が良い。
先程言ったように(1)(2)は8箱周期で①が移動していくということに気がつけばOK。
(3)で箱の種類が絡んできて一気にめんどくさくなりますが、ハッキリ言って問題文の図を見て8箱周期のなかで第1周期では1箱目と5箱目の場所がAの箱で、そこに①が移動して各3回ずつ入るというイメージさえ読み取ることができれば勝ち確定。
あとは掛け算をするだけですが、この8箱周期で考えた場合、第1周期では1箱目と5箱目の場所はちゃんと掛け算した後位置を考えて引き算をしないと死にます。
(ア)で80とか書いてないでしょうね?この辺は集中して解かないといけませんね。
考えているうちにバグってしまった人は頭の中だけで処理せず、手を動かしましょう。
私は簡単な周期表みたいなのを書いて考えました。そうやって書いてみると8箱周期で気をつけなければいけないところが視覚的に認識出来るので思い込みによる数え間違えなどがなくなります。
そうすれば(イ)の問題も①がAに入るのが6個で1周期と考えれば30個はいるのは5つの周期ぴったり。このあたりは出題者の思いやりかな。
ちょっとした工夫(実験してみること)で複雑な思考もシンプルにできますよ。
これ大事です。
昨年度の中期選抜は規則性はただの等差数列だったので、数学が苦手な人はあまりこういう問題は意識せず、規則性の基本パターン(等差や等比、フィボナッチ)を中期選抜までしっかり復習しておきましょう。
まとめ
数学が得意な層に関しては去年の過去問より簡単に感じたかもしれませんね。
問題は標準レベルの層。この子達がどこまでやや難の問題を解ききれているかが気になるところ。
絶妙に出来る層と標準層が命運を分ける難易度設定かなと。
まあ、前期なんでどうでもいいですが。
昨年は中期の難易度はかなり下がってましたので今年も同傾向かと。
今後このレベルの出題傾向が続くならより一層基本問題をしっかり取りきることが大切となりますね。
やっぱりブログで解説(ほとんど解説はしてないが…)はめんどくさい。
解きながら書かないと何時間かたった後だともうどんな問題だったかおぼえてない(笑)
次回は英語です。
今日はこの辺で。
(こちらは2018年2月19日の記事です。)






コメント