
どうも、そいる塾長です。
今日は2019年嵯峨野コスモスの数学を解きながら実況中継風に書いていきます。
傾向と対策を知ってしっかり準備していきましょう!
嵯峨野コスモス2019数学の傾向と対策

100点満点、試験時間50分で大問5~6(小問は17)。あとは1問はかならず「考え方の道筋がわかるように」と過程を記入させる記述問題が出題されます、この辺は普段から意識して取り組む必要がありますね。
ここ5年の出題傾向を見ていると確実に出てくるのは数の性質、関数、平面・空間図形、場合の数・確率の範囲。満遍なく出てますね。この辺は嵯峨野がどうこうではなく、よくある入試問題の傾向。
2018の数学が鬼畜だったので2019年度は合格者平均は専修で71.8、共修で65.1と簡単にしてきましたね。平均が高くなると一問のミスが命取り。一部過程を書く問題を除き、解答が不正解ですと0点になるわけですからね。問題数の少ない数学ではあってはいけません。
あと、こういうときこそ数学が苦手な子には不利です。2018年度みたいなことにすれば一部のぶっとんだ子を除き「中の上」クラス以下が逆に差がつかない。
ということで数学が苦手と思っている方はこういう年こそ差をつけられないように、捨てるところは捨てて標準レベルの問題をしっかりものにすることできちっと6割、しんどいなら5割を取り切って他の科目で勝負できるところまでもっていきましょう。
基本的にここでは、学校で習った知識=教科書に書いてある知識しか使いません。私も塾ではTPOに合わせて高校の知識などを教えたりしますが、○○の定理や△△の公式を理解もせず裏技的に使っていると高校受験で数学が終わりますからね。
ということでできる限り普通の中学生が解ける解法をチョイスしていきたいと思います。それがある意味高校入試では一番スタイリッシュな解法だと思っております。別解などあるかもしれませんが紹介するのはあくまで一つの解法ということで。
そしてあくまで講評に留めますのでがっつり解説は一部のみで、難易度:易に関しては解説をバサッと切り落としていきます。
難易度については、あくまで嵯峨野コスモスを受験する生徒にとっての難易度であり、嵯峨野コスモスの問題内での相対的な評価です。他の専門学科の難易度や共通問題の難易度とは基準が異なることをご理解ください。
簡単に言えば…
- 難易度:易 →解けないと絶望
- 難易度:標準 →解けたら合格ライン
- 難易度:やや難→解けると数学で差がつけられる
- 難易度:難 →解けなくても気にしなーい
という感じにしております。あくまで個人的な見解ですので悪しからず。
ちなみに市販されている嵯峨野コスモスの過去問ではこちら↓がオススメです。志望校なら最新版は購入しておきましょうね。
ちなみにこちら↑の解答は好きじゃないので私の解き方と違うことが多いです。過去問集も色々出ていたりしますので自分にフィットするもので良いかと思います。
では解いていきましょう。
第1問:小問集合
第1問は小問集合。
ここで落とさないように苦手な子は時間をかけてでもきっちり満点をとっていきましょう。
(1)難易度:易 計算の工夫
乗法公式で一発。定期テストの基本問題レベルですね。
(2)難易度:易 一次関数
一次関数の式の決定。これまた定期テストの基本問題レベル。
(3)難易度:易 確率
絵でもかいて丁寧に場合分けすれば簡単。これまた定期テストの基本問題レベル。
(4)難易度:易 円周角
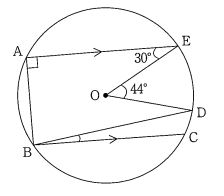
典型的な円周角の問題。中心が描いてあって直角の円周角がある状態でBOに補助線引っ張るなんてまさに定期テストレベルですな。10秒くらいで解いてほしい。
(5)難易度:易 二次関数
これまた増加量と変化の割合というTHE定期テストの問題ですな。
ということで5分くらいで解ける非常に簡単な第1問。満点必須。数学が苦手な人は落ち着いてミスをしないように確実に得点を。得意な人はここで時間を稼いで後半正答率低めの問題を狙っていきましょう。
第2問:平面図形
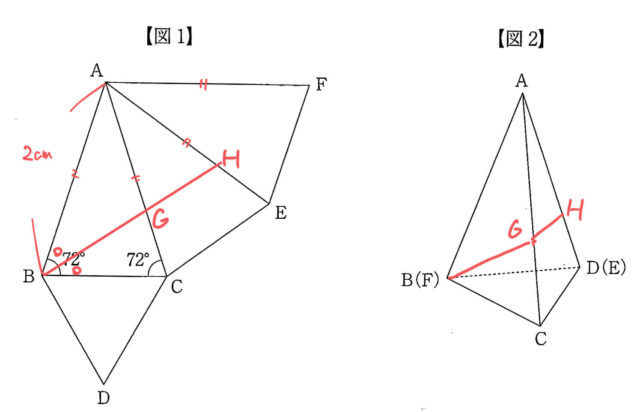
(1)難易度:易
穴抜きでAGの長さの求め方を説明していく問題。誘導が効きすぎているため何も考えなくても空欄が埋まっていってしまいます^^;
(2)難易度:易
AH/AEの値を求める問題。
(1)で求めたAGの長さを使って解こうとすると、ん?俺間違ってる?ってなるくらいに簡単なのでこれでいいのか怖くなった人がたくさんいそうなくらい簡単な問題(私がそうなった…^^;
(3)難易度:標準
正三角錐ABCDの体積(V)とBGHで切断したAを含む方の体積(w)でw/vの値を求める問題。
これみよがしの(1)(2)の誘導にちゃんと乗っかって、図2の三角錐で△ACD(E)を底面にして体積比=底面の面積比っていうのはさすがに子の高校を受けるなら思いつかないといけませんね。思いついてあげないと一生懸命(1)(2)で誘導する問題を作った先生がかわいそうです^^;
第3問:数の性質
問題で小難しそうな定義付けをしておいて考察させる問題。規則性の問題などでもよく出るパターンですね。こういう問題で問われる能力を重視しているんでしょうね。
正確に問題文の設定を読み取らないとその時点で詰んでしまいますが、丁寧に具体例を載せてくれるのでそこまで難しくはないです。
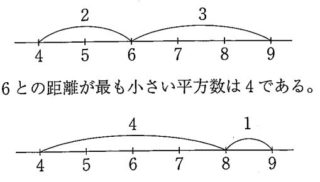
自然数nに対して数直線上でnにもっとも近い平方数との距離をf(n)とする
※f(6)とf(8)の例
(1)難易度:易
f(31)の値
まずは具体的な数字で聞いてくれます。上の定義が理解できれば終わり。
(2)難易度:易
f(n)=3でのnの値
(1)は頭のなかでも出来るとおもいますが(2)のf(n)=3は数直線書いてみましょう。書いても10秒くらいで解けます。こういうのをにらめっこしてるだけで手が動かせない子は勉強方法というか数学という科目と向き合う姿勢から見直した方がいいですよ。
(3)難易度:標準
f(n)=f(n+1)となるnの値(ただし30以下)
普通の中学生ならパッとこの式を見た瞬間戸惑う気持ちは分かるのですが、何のために(1)(2)があるのか考えましょうね。パニクったら落ち着いて実験です。とにかく何かnに数字を入れてみる。試行してみることが何より大切。
まずは問題に書いてあるf(6)の数直線でも見てみればf(6)=f(7)になることはすぐに分かるかと。(なんて易しいんだ嵯峨野高校…。)ということで数直線を問題で求められている30当たりが出てくるまでとにかく書いていれば解けちゃう問題です。
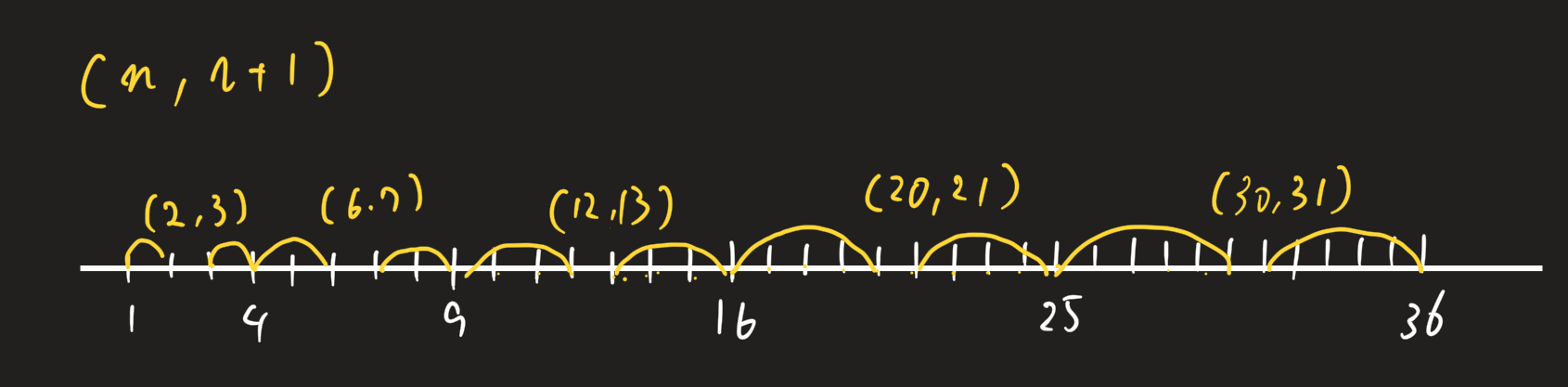
何も全部書かなくとも規則に気が付けば1、4、9、16、25、36と平方数を書き出して隣り合う平方数の和から1引いて2で割った数やんと分かるので全部書くより15秒くらい早く解けるかなw
あえて言うならこの問題で36まで数直線書かず30を答えに書かなかった人はミスとかいうレベルではなく根本から何もこの問題を理解していないので安易におっちょこちょいな私テヘペロ(*´з`)とか言っていないでちゃんと勉強しましょうね。
とにかくフリーズせずに実験。こういう見たことない系は特にそれが大事です。普段から心がけて演習しましょう。
第4問:平面図形
※こちらも図だけ載せておきます。問題文にある情報は書き込んであります。
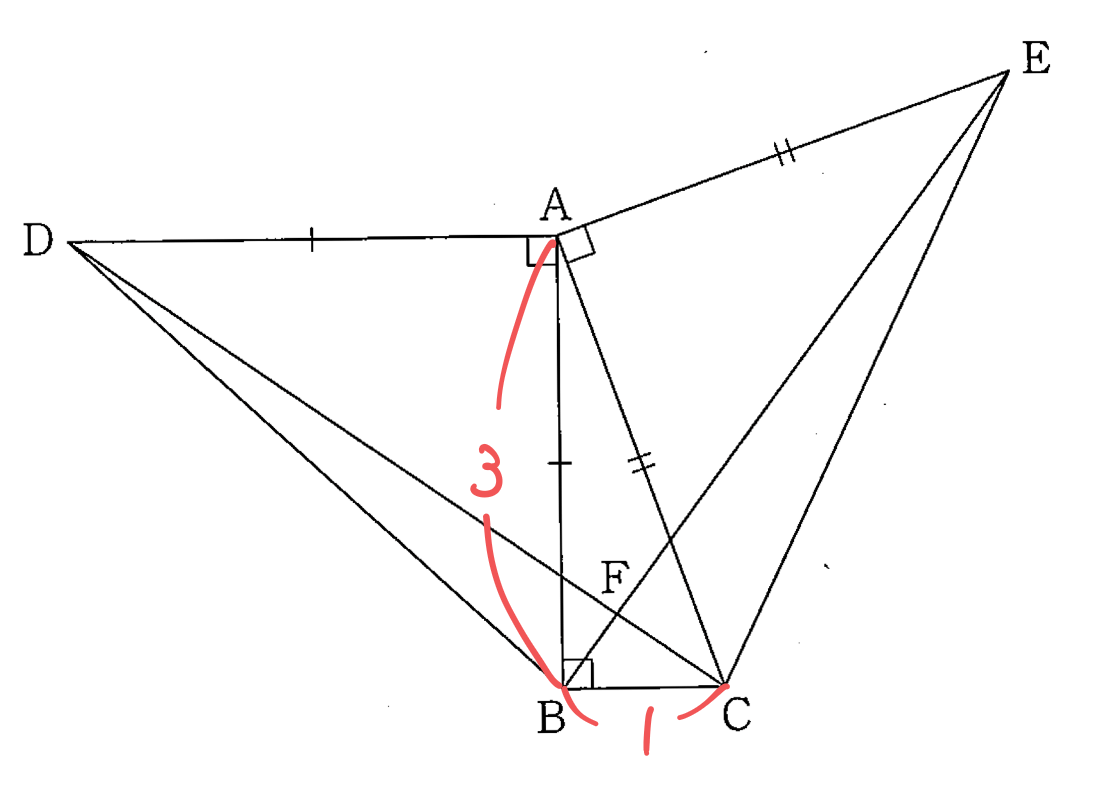
(1)難易度:易
△BCDの面積
小学校か…という問題。
(2)難易度:易
BEの長さ
色んなやり方がありそうですが私は①合同→②相似→③三平方で解きました。
- ①△ADC≡△ABEなので、BE=DC
- ②△ADF∽△BCF(相似比3:1)→AF=9/4、BF=3/4
- ③三平方の定理を用いてDFとFCの長さを出して足してあげる
こんな感じです。非常に基礎的な問題。
(3)難易度:標準
BFの長さ
これも色々解き方はあると思うのですが問題作成者の意図を尊重すると(1)(2)が誘導と考えて乗っかってあげるのがベストかなと。でないとさすがに(1)であの小学生みたいな問題は出さないですよね^^;
ということで今回は(1)で△BCDの面積は何のために出したのかいな?(2)でBE(=CD)の長さをなぜ出したのかな?というところから思考をスタートして考えるとめちゃめちゃ楽に解けるかなと。
- ∠BGF=∠AGD(対頂角)
- ∠GBF=∠ADG(△ADC≡△ABE)
- ∠BGF+∠GBF=90°
よって∠BFG=90°ですね。
第5問:関数
※こちらもグラフだけ載せておきます。問題文にある情報は書き込んであります。
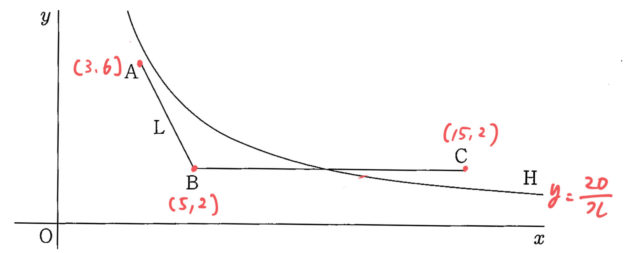
(1)難易度:易
(2)難易度:易
(3)難易度:易
- Pのy座標>Qのy座標のとき(3≦t<10)
- Pのy座標<Qのy座標のとき(10<t≦15)
- 3≦t<5
- 5≦t<10、10<t≦15
これはグラフを見たまんまです。
でこの二つの場合分けを合わせると
- 3≦t<5
- 5≦t<10
- 10<t≦15
となりますね。あとはP、Qの各y座標をそれぞれの場合に合わせて三角形の面積の公式に代入→=2となる方程式を解いていくだけです。
かなり簡単な問題ですね。
場合分け以外、特に記述面で注意する点もありません。
講評





コメント