
どうも、そいる塾長です。
いよいよ明日3月18日は京都公立高校中期選抜の合格発表。
この後春休みくらいのんびりしたい気持ちはわかりますが、進学校はじめ新高1生のみなさんはこの春休みにすでにたくさん課題が出されるかと。
この辺をどうやるか。ただ今までみたいに“提出物”としてこなすだけでいいのか。
ということで高校数学を勉強する心構えを。
今回は数学

どちらかと言えば数学が苦手で、入試では数学が足を引っ張りそうな人向けのお話ですので悪しからず。
数学はおそらく全高1生にとってもっとも学習時間を費やすことになる科目。
もちろんもう現段段階で科目を絞って上位私立大文系を、みたいな人なら知りませんが、少なくとも定期テストでしっかり点数を取るということにおいてもやはり普段から数学にだけは時間をかけておいたほうが良いと思います。でないと数学の副教材とにらめっこしてるだけでテスト1週間が過ぎてしまいます。
もしこれをお読みの方がとても意識の高い方で毎日たっぷり自主学習の時間をとれるようなら全科目予習復習をしっかり行うのが理想です。
しかし殆どの方がそうではない。部活もやらなければいけないし、部活をやっていないからといって勉強に時間を回すとは限りません。
ということで限られた時間を有効活用する方法としても、特に数学が苦手な人は普段から数学に最も時間を割くべきです。間違ってもテスト前に数学の副教材を開くようでは間に合いませんし、そんな人が”あの”数学の副教材の解答で自主学習ができるようには思えません。
最悪の場合、解答配らない自称進学校もあるわけですからね。
だから個別指導の塾にでもということになるわけですが、塾でも中学とは異なり学校の授業である程度は理解してくる前提でないと、週1回の授業で全てカバーするなど不可能です。
ということでどのように勉強していけば良いかお話しますね。とにかく「やってもやってもあがらない」をなくしたい。今回お話するポイントは大きくわけて2つ。
- チャート式数学の使い方
- 教科書+副教材の使い方
最初にチャート式数学の話なんてしてどうすると思われるかもしれませんが、ちょっと理由があります。
1.チャート式数学とは
さて、みなさんもうすぐ学校の教科書などの教材を受け取ります。その中にこんなやつ入ってませんでしたか?
もしも、自分がかなりの難関大学を受けるつもりでないならご愁傷様です。これはもう必要ありません。すぐ返品するか、色違いのものと交換して下さい。
…そんなこと出来ませんけどね(笑)
この青チャート、文系なら東大京大までこの1冊でOKと言われる数学の受験用として知らない人はいない参考書。
ですが、なぜかこれが中堅校~下位校でも買わされるんですよね。
ちなみにこのシリーズは色によって難易度が変わります。
さて自分がこれから通う高校のレベルと受け取ったチャートの色があっているかを確認しましょうね(笑)
他にも緑や紫、黒なども出ていてよりカラフルになっているチャート式ですがその辺はまたどこかでお話するとして今回は学校から配られる可能性のある色のチャートの話に絞ります。
公立高校では、ほとんどが青でしょう。ということはみんな東大京大に行く前提ですね(笑)
はい、返品して白か黄色にして下さい。(出来ませんが^^;
学校の先生はチャートを使ったことがないのでしょうか?これを普段の授業では全く用いず、全く説明もなしにいきなり夏期課題とかで出してきます。
しかも例題だけでなく、EXERCISEを出してくるところも。
1年生で青チャートのEXERCISEが自分でできるならもう東大京大、いや医学部とかもいけるんじゃない?それが偏差値60もない普通の高校で出されるわけですよ。しかも先生が授業するときじゃなく課題として。
もはやテロ!
まず無理ですね。そんなもん無視しましょう。どうせ答え写して終わりです。数学が苦手な人がこんなものを1年生から使えるはずがありません。
進学校では入学前課題でも出されていますね。因数分解くらいまでは簡単だから自分でやって来い的な。
いやいやそこはちゃんと授業でやらんといかんぜよって思うんですけどね。
最初は簡単。でも今後の全てを決める大切な要素が詰まっているわけです。そこを飛ばす精神が私には理解できないんですよね。塾なんかに通っている方はいいんですが、そうでないとどうやって勉強するかもわからないのではないでしょうか?
せめてやり方まとめたプリントくらい配れよと。
本当は全員白からスタートしても良いくらいです。いや、定期テストのためには白を買い直しても良いのではないでしょうか?
私的には教科書よりはわかりやすい気もしないではない。少なくともできたら学校に逆らってでも自分にあった色のチャート式を使ってほしいところです。
チャート式数学の勉強法
では肝心のチャート式数学の使い方です。
間違ってほしくないのは白チャートでもない限り、このシリーズは受験対策用です。数学が分からなくなったから読むわかりやすい参考書ではないです。
あえていうなら辞書かな。教科書⇄チャート、4stepやサクシード⇄チャート、過去問⇄チャートっていうイメージでしょうか。
受験用参考書としては、賛否両論ありますが、私個人の経験から言うと青チャートと過去問だけで京大の文系数学は高得点がとれましたので十分なスペックはあると思います。
また私が使い慣れているからかもしれませんが、そのページレイアウトも使いやすいように思います。1頁に例題がぴったり1問は見やすい(私は参考書においては視認性を大事にするからなんですが。)
青チャートの使い方にはわりと精通しているつもりですが、今回はそんなにハイレベルな入試数学の話をするつもりはありません。
あくまで数学が苦手な子が高校数学を学ぶためのお作法の話です。
そんな子にチャート式を使って勉強しろというわけではありません。あくまでチャート式数学の例題のところのページレイアウトが数学の問題を理解していく上で大変参考になるので、最初にチャート式数学のお話をするというわけです。
そもそもチャートがお勧めです!というより「あー、チャートをもらっちゃったのね。じゃせっかくですし・・・」という姿勢(笑)
なおチャート式数学のページはこうなっています。

ポイントは赤字のCHARTのところ。その上の指針のところをまとめたような言葉が書いています。
ここが問題を解く上での着眼点というか、安易な言葉でいうとパターンでしょうか。ただし、数学が解けない人がこの赤字を丸暗記しても全く解けないと思います。
つまりパターン暗記をしろと言っているわけではありませんのでご注意を。
ここで重要なのは、この赤字の日本語がいったい数学の世界ではどういう意味を持つのかということ、そしてそれを使う理由、それを使うことで何が起きるのかを実際に解答をすすめる上でしっかりと理解することが大切です。パターンを暗記するのではなく、その問題にある出題者の意図を理解する。
この画像のページは実際にこないだの新高1スタートダッシュ講座でやった数学の問題です。例えばここには…
CHART「文字の次数が同じなら、一つの文字について整理」
この問題をチョイスしたポイントは使う知識はすべて中学数学の範囲内であること。
なのにチャート式の赤字の部分を理解していないと解けない問題です。
できる子ほど、途中で「あー!」って感じになっていきます。
「一つの文字について整理」という言葉をおぼえるのではなく、一つの文字について整理すると何が起きるのか理解するのです。
それがなんで「一つの文字について整理する」のかということです。
この「あー!」って感じが見えたからならOK。
(ならなければ中学数学の復習は必要ですね。◀の共通因数でくくるのが出てこないのは問題。)
数学をやらなければできるようにならないのは当たり前ですが、やってもやっても上がらないという人が多いのも数学。そういう人はだいたいひたすら問題を解く⇒解答丸暗記というパターン。
これではただの作業。テスト前に勉強したのに試験当日出来ない、というのもこれが原因。
たとえこの赤字のCHARTの部分であっても丸暗記では何の役にも立たないわけです。
あと解答の右にある◀の部分。ここも普通の解答よりもなぜその式になるのかが書いてあって助かる。
同じ赤字のCHARTの問題でも最後までそれ一本で解けるわけではなく、サブテーマみたいなものがあります。それがこの◀の部分に書かれています。
例えば今回の部分では「共通因数」のとこ。ちなみに次のページではここが「たすき掛け」にかわります。
「共通因数」はできても「たすき掛け」だと解けないなら今身につけるべきは「たすき掛け」の着眼点になりますね。
ですのでここも赤字のCHARTと同じように処理していけばよいですね。
たすき掛けや平方完成はただの計算テクニックでいいの?
私が高1生の数学の授業でやるのは先取りじゃないです。
例えばたすき掛けのやり方を教えますがそれは放っておいても学校で学ぶし、それが理解できない人はいません。だってそれは「やり方」だから。
「やり方」というものは慣れればできる。
だけどそこで本当に大切なのは「やり方」ではなく「なんでそうなるの?」という視点。
それがないとおそらくその後の複雑な因数分解はまた別の「やり方」の暗記になります。
それを防ぎたい。
平方完成もそれですね。いやこっちはもう少し深いか。
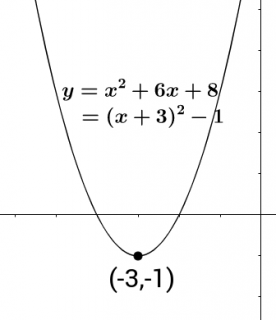
上の画像はスタディプラスさんのサイトより引用させてもらいました。
なぜこの形で頂点だとわかるのか。平行移動や不等式のところまで平方完成から思考を延ばせるか。そもそも平方にすると色々わかるよね?これって中3でもやったよね?平方ってワクワクするよね?(それはどうでもいい・・・^^;)そういった視点をあの式変形ひとつから読み取った上で身につけてもらいたい。
一つの式からちゃんと色んなイメージに繋げられるか。これってこの後の数学で大事になるんじゃないかなと。
もちろんたすき掛けも平方完成もとても大事な「計算方法」 。だから無意識レベルで瞬時にできるように身につけて欲しい。ただ式変形するだけの「やり方」ならば心を無にしてひたすら計算ドリルでもやればいい。
でも高校数学の面白さってそこじゃないでしょうと。
そんな話をダラダラするのが私の春期講習です(^◇^;)
参考書には書き込め
問題部分は書き込みご法度ですが、なぜ解説部分に書き込まないのか。
たとえばどこまで解けたかを書き込むだけでも違ってくるし、もっと重要なのは頭の中でこねくり回したことを言語化して書き込んでおくことです。
チャートなんかは1回解いておしまいなんてことはあるわけでなく何度も何度もとき直すわけです。そのたびにまた0からこねくり回してる場合じゃない。
それに解説を読んで自分なりに生み出した思考を言語化してアウトプットするのはとても大切です。
もちろん先生に質問して教えてもらったことは言うまでもありません。
わかったからOK。みたいな勉強をする人が多いですが、自分で一から解き切ったわけでもない限りほとんどの場合理解はしていないし、解けたとしてもパターン暗記してそのパターンにハメて解いただけなら理解などしていない。
そのあたりの「自分が本当にわかっているのかどうか」を自分でわかることが本当の勉強です。
教科書と副教材の問題集の使い方
本来は新高1生にはこちらから話をすべきであることは承知しています。
特に副教材はどの学校でも扱いますが、チャート式で授業するところはありませんし、先程書いたようにチャートはあくまで受験用。
しかし、チャート式の使い方で書いた赤字の部分のお話。あの赤字をどうやってこの副教材で見つけていくかが重要だと思っています。
残念ながら、このような教材の解答は決して丁寧とは言えません。ただひたすらに解答が書いてあるだけです。だからそれを自分で考えて見つけるなんて至難の技です。
ではどうすればできるのか?
そのために教科書と学校の授業はある。ということですね。
だからこそ、しっかり教科書をしっかり読んで授業を受け、その授業の範囲については遅くとも次回授業までに副教材で演習を行うということです。
もちろんそれをチャートから類似問題を探してやるのでもよいのですが、そのときに青チャートではレベルが高すぎる可能性があるので、苦手な人は白チャートを自前で用意しておくほうが良いかもしれません。
私がやっていたのは(過去問演習のときですが)自分が解けなかった問題に関しては解説を読み自分でチャート式における赤字の部分や、補足の部分を自分で作成したノートを作るということです。
そこまで普段の学習では出来ないという人はせめて教科書や副教材の解答部分にでもそういったものを書き込んではいかがでしょうか。
(話が重複しますが)数学ができない人はその場で答えがわかれば良いという風になっていて、自分の考えたことを何も書き込まない。
ノートには解答に必要な数式と計算が書いてあるだけでその数式や計算を生み出す考え方が書いていないのです。
それが自分で考えついたものであれば良いのですが、何かを見てわかったのであったり、誰かに教えてもらってわかったのであれば、絶対に書きとめておきましょう。
間違いなく数日後にわからなくなります。
もう一度解くとき、再度同じように考えて解答ができるようにしておかなければ反復練習になりません。
できる限り、自分の頭の中で起こったことは言語化して残していく。
これをするだけで必ず考える力がつきます。
逆に何を書けばよいか分からないとなる場合、ほぼ確実に答えがわかっただけで問題を理解してはいません。
本当に理解しているかどうかという事自体を「理解」することが大切です。
その昔、質問箱で昔数学のセンスはどうやったら身につきますかという質問を受けました。
私は数学がわりと得意科目でしたが、センスなんて欠片もありませんでした。
ただし問題をといて丸暗記など絶対にしなかった。
ひたすらチャートや過去問の問題、そして解答を頭の中でこねくり回し、なんでその式になるのか?なんでそれが思いつくのか?その式に一体どういう意味があるのか?ひたすら考えるんです。そして手を動かし続けるのです。
それをひたすら繰り返しているうちに数学の問題を解くうえで必要な見方や考え方が身についたというほかありません。
ひたすら問題を解くのではなく、ひたすら考えて下さい。自分のわからないと真剣にぶつかって頭と手を動かしましょう。
絶対に勉強を作業にしてはいけません。
抽象的な話になってしまって申し訳ないですが数学の勉強作法はこの「考える」という作業です。
ということで、今日はこのへんで。




コメント